如何来构建神经网络？看看这篇干货

共计 6469 个字符，预计需要花费 17 分钟才能阅读完成。

导读	在这篇文章中，您将学习图神经网络如何工作的基础知识，以及如何使用 Pytorch Geometric（PyG）库和 Open Graph Benchmark（OGB）库并通过 Python 编程实现这样一个图神经网络。

如何来构建神经网络？看看这篇干货
深度学习为对非结构化数据进行预测开辟了一个全新的可能性世界。如今，人们常用卷积神经网络（CNN）处理图像数据，而采用递归神经网络（RNN）来处理文本数据，等等。

在过去几年中，又出现了一类新的令人兴奋的神经网络：图神经网络（Graph Neural Networks，简称“GNN”）。顾名思义，这个网络类型专注于处理图数据。

在这篇文章中，您将学习图神经网络如何工作的基础知识，以及如何使用 Pytorch Geometric（PyG）库和 Open Graph Benchmark（OGB）库并通过 Python 编程实现这样一个图神经网络。

注意，您可以在我的 Github 和 Kaggle 网站上找到本文提供的示例工程源码。

普通 GNN 的工作原理

随着图卷积网络（GCN）[见参考文献 1]的引入，GNN 开始流行起来，该网络将 CNN 中的一些概念借用到了图世界。这种网络的主要思想，也称为消息传递框架（Message-Passing Framework），多年来成为该领域的黄金标准。我们将在本文中探讨这一概念。

消息传递框架指出，对于图中的每个节点，我们将做两件事：

聚合来自其邻节点的信息
使用来自其上一层及其邻节点聚合的信息更新当前节点信息
如何来构建神经网络？看看这篇干货

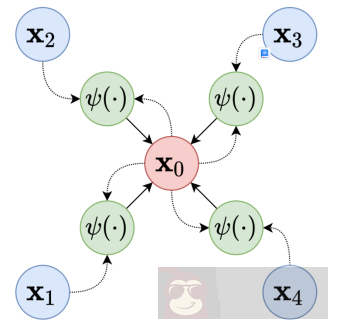
消息传递框架示意图。来源：维基百科

上图中显示了消息传递框架的工作原理。在 GCN 之后开发的许多架构侧重于定义聚合和更新数据的最佳方式。

PyG 和 OGB 简介

PyG 是 Pytorch 库的扩展，它允许我们使用研究中已经建立的层快速实现新的图神经网络架构。

OGB[见参考文献 2]是作为提高该领域研究质量的一种方式开发的，因为它提供了可使用的策划图，也是评估给定架构结果的标准方式，从而使提案之间的比较更加公平。

于是，我们可以将这两个库一起使用，一方面可以更容易地提出一个架构，另一方面也不必担心数据获取和评估机制的问题。

实现一个 GNN 项目

首先，让我们安装示例工程必需的库。请注意，您必须首先安装 PyTorch：

pip install ogb
pip install torch_geometric

现在，让我们导入所需的方法和库：

import os
import torch
import torch.nn.functional as Ffrom tqdm import tqdm
from torch_geometric.loader import NeighborLoader
from torch.optim.lr_scheduler import ReduceLROnPlateau
from torch_geometric.nn import MessagePassing, SAGEConv
from ogb.nodeproppred import Evaluator, PygNodePropPredDataset

接下来，第一步是从 OGB 下载数据集。我们将使用 ogbn-arxiv 网络，其中每个节点都是 arxiv 网站上的计算机科学论文，每个有向边表示一篇论文引用了另一篇论文。我们的任务是：将每个节点分类为一个论文类别。

下载过程非常简单：

target_dataset = 'ogbn-arxiv'# 我们将把 ogbn-arxiv 下载到当前示例工程的 'networks' 文件夹下
dataset = PygNodePropPredDataset(name=target_dataset, root='networks')

其中，dataset 变量是一个名为 PygNodePropPredDataset 的类的实例，该类特定于 OGB 库。要将该数据集作为可在 Pyrotch Geometric 上使用的数据类进行访问，我们只需执行以下操作：

data = dataset[0]

如果我们通过调试跟踪看一下这个变量，我们会看到如下结果：

Data(num_nodes=169343, edge_index=[2, 1166243], x=[169343, 128], node_year=[169343, 1], y=[169343, 1])

至此，我们已经准备好了节点数目、邻接列表、网络的特征向量、每个节点的年份信息，并确定下目标标签。

另外，ogbn-arxiv 网络已经配备好了分别用于训练、验证和测试的分割数据子集。这是 OGB 提供的一种提高该网络研究再现性和质量的好方法。我们可以通过以下方式提取：

split_idx = dataset.get_idx_split() 
        
train_idx = split_idx['train']
valid_idx = split_idx['valid']
test_idx = split_idx['test']

现在，我们将定义两个在训练期间使用的数据加载器。第一个将仅加载训练集中的节点，第二个将加载网络上的所有节点。

我们将使用 Pytorch Geometric 库中的邻节点加载函数 NeighborLoader。该数据加载器为每个节点采样给定数量的邻节点。这是一种避免具有数千个节点的节点的 RAM 和计算时间瘫痪的方法。在本教程中，我们将在训练加载程序上每个节点使用 30 个邻节点。

train_loader = NeighborLoader(data, input_nodes=train_idx,
                              shuffle=True, num_workers=os.cpu_count() - 2,
                              batch_size=1024, num_neighbors=[30] * 2)total_loader = NeighborLoader(data, input_nodes=None, num_neighbors=[-1],
                               batch_size=4096, shuffle=False,
                               num_workers=os.cpu_count() - 2)

注意，我们把训练数据加载器中的数据以随机方式打乱次序，但没有打乱总加载器中数据的次序。此外，训练加载程序的邻节点数定义为网络每层的数量。因为我们将在这里使用两层网络，所以我们将其设置为两个值为 30 的列表。

现在是时候创建我们的 GNN 架构了。对于任何熟悉 Pytorch 的人来说，这应该都是平常的事情。

我们将使用 SAGE 图层。这些层是在一篇很好的论文[见参考文献 3]中定义的，该论文非常细致地介绍了邻节点采样的思想。幸运的是，Pytorch Geometric 库已经为我们实现了这一层。

因此，与每个 PyTorch 架构一样，我们必须定义一个包含我们将要使用的层的类：

class SAGE(torch.nn.Module):
    def __init__(self, in_channels,
                 hidden_channels, out_channels,
                 n_layers=2):
        
        super(SAGE, self).__init__()
        self.n_layers = n_layers    self.layers = torch.nn.ModuleList()
        self.layers_bn = torch.nn.ModuleList()    if n_layers == 1:
            self.layers.append(SAGEConv(in_channels, out_channels,   normalize=False))
        elif n_layers == 2:
            self.layers.append(SAGEConv(in_channels, hidden_channels, normalize=False))
             self.layers_bn.append(torch.nn.BatchNorm1d(hidden_channels))
            self.layers.append(SAGEConv(hidden_channels, out_channels, normalize=False))
        else:
           self.layers.append(SAGEConv(in_channels, hidden_channels, normalize=False))
              self.layers_bn.append(torch.nn.BatchNorm1d(hidden_channels))    for _ in range(n_layers - 2):
                self.layers.append(SAGEConv(hidden_channels,  hidden_channels, normalize=False))
                 self.layers_bn.append(torch.nn.BatchNorm1d(hidden_channels))
            
            self.layers.append(SAGEConv(hidden_channels, out_channels, normalize=False))
            
        for layer in self.layers:
            layer.reset_parameters()    def forward(self, x, edge_index):
        if len(self.layers) > 1:
            looper = self.layers[:-1]
        else:
            looper = self.layers
        
        for i, layer in enumerate(looper):
            x = layer(x, edge_index)
            try:
                x = self.layers_bn[i](x)
            except Exception as e:
                abs(1)
            finally:
                x = F.relu(x)
                x = F.dropout(x, p=0.5, training=self.training)
        
        if len(self.layers) > 1:
            x = self.layers[-1](x, edge_index)        return F.log_softmax(x, dim=-1), torch.var(x)
    
    def inference(self, total_loader, device):
        xs = []
        var_ = []
        for batch in total_loader:
            out, var = self.forward(batch.x.to(device), batch.edge_index.to(device))
            out = out[:batch.batch_size]
            xs.append(out.cpu())
            var_.append(var.item())
        
        out_all = torch.cat(xs, dim=0)
        
        return out_all, var_

让我们一步一步地将上述代码分开解释：

我们必须定义网络的 in_channels 数量，这个值代表数据集中的特征数。out_channels 代表我们试图预测的类别的总数。隐藏通道参数 idden_channels 是一个我们可以定义的值，表示隐藏单元的数量。
我们可以设置网络的层数。对于每个隐藏层，我们添加一个批量归一化层，然后重置每个层的参数。
forward 方法运行正向过程的单个迭代。期间，获得特征向量和邻接列表，并将其传递给 SAGE 层，然后将结果传递给批量归一化层。此外，我们还应用 ReLU 非线性和衰减层进行正则化。
最后，推理方法（inference）将为数据集中的每个节点生成预测。我们将使用它进行验证。
现在，让我们定义模型的一些参数：

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')model = SAGE(data.x.shape[1], 256, dataset.num_classes, n_layers=2)
model.to(device)
epochs = 100
optimizer = torch.optim.Adam(model.parameters(), lr=0.03)
scheduler = ReduceLROnPlateau(optimizer, 'max', patience=7)

现在，我们可以开始测试了，以验证我们的所有预测：

def test(model, device):
    evaluator = Evaluator(name=target_dataset)
    model.eval()
    out, var = model.inference(total_loader, device)    y_true = data.y.cpu()
        y_pred = out.argmax(dim=-1, keepdim=True)    train_acc = evaluator.eval({'y_true': y_true[split_idx['train']],
        'y_pred': y_pred[split_idx['train']],
    })['acc']
    val_acc = evaluator.eval({'y_true': y_true[split_idx['valid']],
        'y_pred': y_pred[split_idx['valid']],
    })['acc']
    test_acc = evaluator.eval({'y_true': y_true[split_idx['test']],
        'y_pred': y_pred[split_idx['test']],
    })['acc']return train_acc, val_acc, test_acc, torch.mean(torch.Tensor(var))

在这个函数中，我们从 OGB 库中实例化一个验证器类 Validator。这个类将负责验证我们之前检索到的每个分割的模型。这样，我们将看到每个世代上的训练、验证和测试集的得分值。

最后，让我们创建我们的训练循环：

for epoch in range(1, epochs):
    model.train()    pbar = tqdm(total=train_idx.size(0))
    pbar.set_description(f'Epoch {epoch:02d}')    total_loss = total_correct = 0    for batch in train_loader:
        batch_size = batch.batch_size
        optimizer.zero_grad()        out, _ = model(batch.x.to(device), batch.edge_index.to(device))
        out = out[:batch_size]        batch_y = batch.y[:batch_size].to(device)
        batch_y = torch.reshape(batch_y, (-1,))        loss = F.nll_loss(out, batch_y)
        loss.backward()
        optimizer.step()        total_loss += float(loss)
        total_correct += int(out.argmax(dim=-1).eq(batch_y).sum())
        pbar.update(batch.batch_size)    pbar.close()    loss = total_loss / len(train_loader)
    approx_acc = total_correct / train_idx.size(0)    train_acc, val_acc, test_acc, var = test(model, device)
    
    print(f'Train: {train_acc:.4f}, Val: {val_acc:.4f}, Test: {test_acc:.4f}, Var: {var:.4f}')

这个循环将训练我们的 GNN 的 100 个世代，如果我们的验证得分连续 7 个世代没有增长的话，它将提前停止训练。

结论

总之，GNN 是一类有趣的神经网络。今天，人们已经开发出了一些现成的工具来帮助我们开发这种解决方案。正如您在本文中所见到的，借助 Pytorch Geometric 和 OGB 这两个库就可以轻松实现某些类型的图的 GNN 设计。