常用的限流框架

共计 3416 个字符，预计需要花费 9 分钟才能阅读完成。

一般的限流常常需要指定一个固定值 (qps) 作为限流开关的阈值，这个值一是靠经验判断，二是靠通过大量的测试数据得出。但这个阈值，在流量激增、系统自动伸缩或者某某 commit 了一段有毒代码后就有可能变得不那么合适了。并且一般业务方也不太能够正确评估自己的容量，去设置一个合适的限流阈值。

而此时自适应限流就是解决这样的问题的，限流阈值不需要手动指定，也不需要去预估系统的容量，并且阈值能够随着系统相关指标变化而变化。

自适应限流算法借鉴了 TCP 拥塞算法，根据各种指标预估限流的阈值，并且不断调整。大致获得的效果如下:

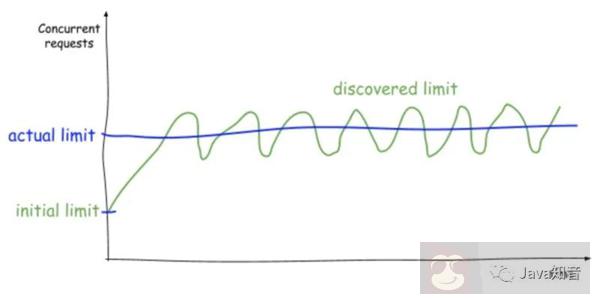
从图上可以看到，首先以一个降低的初始并发值发送请求，同时通过增大限流窗口来探测系统更高的并发性。而一旦延迟增加到一定程度了，又会退回到较小的限流窗口。循环往复持续探测并发极限，从而产生类似锯齿状的时间关系函数。

vegas 是一种主动调整 cwnd 的拥塞控制算法，主要是设置两个阈值 alpha 和 beta，然后通过计算目标速率和实际速率的差 diff，再比较差 diff 与 alpha 和 beta 的关系，对 cwnd 进行调节。伪代码如下：

diff = cwnd*(1-baseRTT/RTT)  
if (diff = beta)  
set: cwndcwnd = cwnd - 1  
else  
set: cwndcwnd = cwnd

其中 baseRTT 指的是测量的最小往返时间，RTT 指的是当前测量的往返时间，cwnd 指的是当前的 TCP 窗口大小。通常在 tcp 中 alpha 会被设置成 2 -3，beta 会被设置成 4 -6。这样子，cwnd 就保持在了一个平衡的状态。

concuurency-limits 是 netflix 推出的自适应限流组件，借鉴了 TCP 相关拥塞控制算法，主要是根据请求延时，及其直接影响到的排队长度来进行限流窗口的动态调整。

vegas 算法实现在了 VegasLimit 类中。先看一下初始化相关代码:

private int initialLimit = 20;  
        private int maxConcurrency = 1000;  
        private MetricRegistry registry = EmptyMetricRegistry.INSTANCE;  
        private double smoothing = 1.0;         
        private Function alphaFunc = (limit) -> 3 * LOG10.apply(limit.intValue());  
        private Function betaFunc = (limit) -> 6 * LOG10.apply(limit.intValue());  
        private Function thresholdFunc = (limit) -> LOG10.apply(limit.intValue());  
        private Function increaseFunc = (limit) -> limit + LOG10.apply(limit.intValue());  
        private Function decreaseFunc = (limit) -> limit - LOG10.apply(limit.intValue()); 

这里首先定义了一个初始化值 initialLimit 为 20，以及极大值 maxConcurrency1000。其次是三个阈值函数 alphaFunc，betaFunc 以及 thresholdFunc。最后是两个增减函数 increaseFunc 和 decreaseFunc。

函数都是基于当前的并发值 limit 做运算的。

alphaFunc 可类比 vegas 算法中的 alpha，此处的实现是 3 *log limit。limit 值从初始 20 增加到极大 1000 时候，相应的 alpha 从 3.9 增加到了 9。

betaFunc 则可类比为 vegas 算法中的 beta，此处的实现是 6 *log limit。limit 值从初始 20 增加到极大 1000 时候，相应的 alpha 从 7.8 增加到了 18。

thresholdFunc 算是新增的一个函数，表示一个较为初始的阈值，小于这个值的时候 limit 会采取激进一些的增量算法。这里的实现是 1 倍的 log limit。mit 值从初始 20 增加到极大 1000 时候，相应的 alpha 从 1.3 增加到了 3。

这三个函数值可以认为确定了动态调整函数的四个区间范围。当变量 queueSize = limit × (1 − RTTnoLoad/RTTactual)落到这四个区间的时候应用不同的调整函数。

其中变量为 queueSize，计算方法即为 limit × (1 − RTTnoLoad/RTTactual)，为什么这么计算其实稍加领悟一下即可。

我们把系统处理请求的过程想象为一个水管，到来的请求是往这个水管灌水，当系统处理顺畅的时候，请求不需要排队，直接从水管中穿过，这个请求的 RT 是最短的，即 RTTnoLoad；

反之，当请求堆积的时候，那么处理请求的时间则会变为：排队时间 + 最短处理时间，即 RTTactual = inQueueTime + RTTnoLoad。而显然排队的队列长度为

总排队时间 / 每个请求的处理时间及 queueSize = (limit * inQueueTime) / (inQueueTime + RTTnoLoad) = limit × (1 − RTTnoLoad/RTTactual)。

再举个栗子，因为假设当前延时即为最佳延时，那么自然是不用排队的，即 queueSize=0。而假设当前延时为最佳延时的一倍的时候，可以认为处理能力折半，100 个流量进来会有一半即 50 个请求在排队，及 queueSize= 100 * (1 − 1/2)=50。

调整函数中最重要的即增函数与减函数。从初始化的代码中得知，增函数 increaseFunc 实现为 limit+log limit，减函数 decreaseFunc 实现为 limit-log limit，相对来说增减都是比较保守的。

看一下应用动态调整函数的相关代码：

private int updateEstimatedLimit(long rtt, int inflight, boolean didDrop) {final int queueSize = (int) Math.ceil(estimatedLimit * (1 - (double)rtt_noload / rtt));  
        double newLimit;  
        // Treat any drop (i.e timeout) as needing to reduce the limit  
        // 发现错误直接应用减函数 decreaseFunc  
        if (didDrop) {newLimit = decreaseFunc.apply(estimatedLimit);  
        // Prevent upward drift if not close to the limit  
        } else if (inflight * 2  beta) {newLimit = decreaseFunc.apply(estimatedLimit);  
            // We're within he sweet spot so nothing to do  
            } else {return (int)estimatedLimit;  
            }  
        }  
        newLimit = Math.max(1, Math.min(maxLimit, newLimit));  
        newLimit = (1 - smoothing) * estimatedLimit + smoothing * newLimit;  
        if ((int)newLimit != (int)estimatedLimit && LOG.isDebugEnabled()) {LOG.debug("New limit={} minRtt={} ms winRtt={} ms queueSize={}",  
                    (int)newLimit,  
                    TimeUnit.NANOSECONDS.toMicros(rtt_noload) / 1000.0,  
                    TimeUnit.NANOSECONDS.toMicros(rtt) / 1000.0,  
                    queueSize);  
        }  
        estimatedLimit = newLimit;  
        return (int)estimatedLimit;  
    }

动态调整函数规则如下：

当变量 queueSize