共计 4071 个字符,预计需要花费 11 分钟才能阅读完成。

排序是我们生活中经常会面对的问题,体育课的时候,老师会让我们从矮到高排列,考研录取时,成绩会按总分从高到底进行排序(考研的各位读者,你们必能收到心仪学校给你们寄来的大信封),我们网购时,有时会按销量从高到低,价格从低到高的顺序将最符合咱们预期的商品列在前面,这些都是我们生活中的例子。
排序概念:将杂乱无章的数据元素,通过一定的方法 (排序算法) 按关键字顺序排列的过程叫做排序。例如我们上面的销量和价格就是关键字。
因为我们待排序的记录序列中可能存在两个或两个以上的关键字相等的记录,排序结果可能会存在不唯一的情况,所以我们排序之后,如果相等元素之间原有的先后顺序不变。则称所用的排序方法是稳定的,反之则称之为不稳定的。见下图
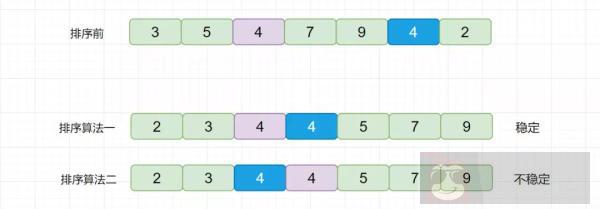
例如上图,我们的数组中有两个相同的元素 4,我们分别用不同的排序算法对其排序,算法一排序之后,两个相同元素的相对位置没有发生改变,我们则称之为稳定的排序算法,算法二排序之后相对位置发生改变,则为不稳定的排序算法。
在我们刷题中大多只是将数组进行排序,只需考虑时间复杂度,空间复杂度等指标,排序算法是否稳定,一般不进行考虑。但是在真正软件开发中排序算法的稳定性是一个特别重要的衡量指标。继续说我们刚才的例子。我们想要实现年终奖从少到多的排序,然后相同年终奖区间内的红豆数也按照从少到多进行排序。
排序算法的稳定性在这里就显得至关重要。这是为什么呢? 见下图
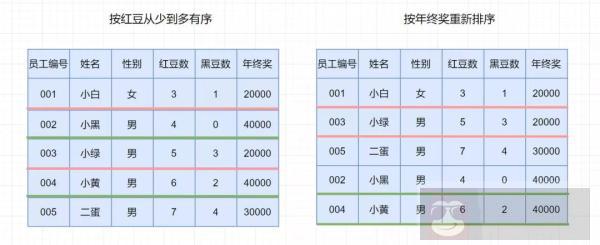
第一次排序之后,所有的职工按照红豆数从少到多有序。
第二次排序中,我们使用稳定的排序算法,所以经过第二次排序之后,年终奖相同的职工,仍然保持着红豆的有序(相对位置不变),红豆仍是从小到大排序。我们使用稳定的排序算法,只需要两次排序即可。
稳定排序可以让第一个关键字排序的结果服务于第二个关键字排序中数值相等的那些数。
上述情况如果我们利用不稳定的排序算法,实现这一效果是十分复杂的。
我们根据元素是否依靠与其他元素的比较来决定元素间的相对次序。以此来区分比较类排序算法和非比较类排序算法。
内排序是在排序的整个过程中,待排序的所有记录全部被放置在内存中。外排序是由于排序的记录个数太多,不能同时放置在内存中,整个排序过程需要在内外存之间多次交换数据才能进行,常见的内部排序算法有:插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。
对我们内排序来说,我们主要受三个方面影响,时间性能,辅助空间,算法的复杂性
在我们的排序算法执行过程中,主要执行两种操作比较和交换,比较是排序算法最起码的操作,移动指记录从一个位置移动到另一个位置。所以我们一个高效的排序算法,应该尽可能少的比较和移动。
执行算法所需要的辅助空间的多少,也是来衡量排序算法性能的一个重要指标
这里的算法复杂度不是指算法的时间复杂度,而是指算法本身的复杂度,过于复杂的算法也会影响排序的性能。
下面我们一起先来复习两种简单排序算法,冒泡排序和简单选择排序,看看有没有之前忽略的东西。后面会持续连载,把常见的和实用的排序算法都进行总结。
我们在各个算法书上学习排序时,第一个估计都是冒泡排序。主要是这个排序算法思路最简单,也最容易理解,(也可能是它的名字好听,哈哈),学过的老哥们也一起来复习一下吧,我们一起深挖一下冒泡排序。
冒泡排序的基本思想是,两两比较相邻记录的关键字,如果是反序则交换,直到没有反序为止。冒泡排序一次冒泡会让至少一个元素移动到它应该在的位置,那么如果数组有 n 个元素,重复 n 次后则一定能完成排序。根据定义可知那么冒泡排序显然是一种比较类排序。
我们先来看一下这段代码
| class Solution {public int[] sortArray(int[] nums) { | |
| int len = nums.length; | |
| for (int i = 0; i nums[j]) {swap(nums,i,j); | |
| } | |
| } | |
| } | |
| return nums; | |
| } | |
| public void swap(int[] nums,int i,int j) {int temp = nums[i]; | |
| nums[i] = nums[j]; | |
| nums[j] = temp; | |
| } | |
| } |
我们来思考一下上面的代码,每次让关键字 nums[i] 和 nums[j] 进行比较如果 nums[i] > nums[j] 时则进行交换,这样 nums[0] 在经过一次循环后一定为最小值。
那么这段代码是冒泡排序吗? 显然不是,我们冒泡排序的思想是两两比较相邻记录的关键字,注意里面有相邻记录,所以这段代码不是我们的冒泡排序,下面我们用动图来模拟一下冒泡排序的执行过程,看完之后一定可以写出正宗的冒泡排序。
| class Solution {public int[] sortArray(int[] nums) { | |
| int len = nums.length; | |
| for (int i = 0; i nums[j+1]) {swap(nums,j,j+1); | |
| } | |
| } | |
| } | |
| return nums; | |
| } | |
| public void swap(int[] nums,int i,int j) {int temp = nums[i]; | |
| nums[i] = nums[j]; | |
| nums[j] = temp; | |
| } | |
| } |
上图中的代码则为正宗的冒泡排序代码,但是我们是不是发现了这个问题
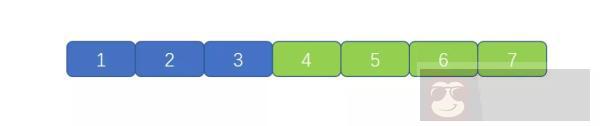
我们此时数组已经完全有序了,可以直接返回,但是动图中并没有返回,而是继续执行,那我们有什么办法让其完全有序时,直接返回,不继续执行呢?
我们设想一下,我们是通过 nums[j] 和 nums[j+1] 进行比较,如果大于则进行交换,那我们设想一下,如果一个完全有序的数组,我们进行冒泡排序,每次比较发现都不用进行交换。那么如果没有发生交换则说明当前完全有序。
那我们可不可以通过一个标志位来进行判断是否发生了交换呢? 当然是可以的
我们来对冒泡排序进行改进
| class Solution {public int[] sortArray (int[] nums) { | |
| int len = nums.length; | |
| // 标志位 | |
| boolean flag = true; | |
| // 注意看 for 循环条件 | |
| for (int i = 0; i nums[j+1]) {swap(nums,j,j+1); | |
| // 发生交换,则变为 true, 下次继续判断 | |
| flag = true; | |
| } | |
| } | |
| } | |
| return nums; | |
| } | |
| public void swap (int[] nums,int i,int j) {int temp = nums[i]; | |
| nums[i] = nums[j]; | |
| nums[j] = temp; | |
| } | |
| } |
这样我们就避免掉了已经有序的情况下无意义的循环判断。
最好情况,就是要排序的表完全有序的情况下,根据改进后的代码,我们只需要一次遍历即可,只需 n -1 次比较,时间复杂度为 O(n)。
最坏情况时,即待排序表逆序的情况,则需要比较(n-1) + (n-2) +…. + 2 + 1= n*(n-1)/2,并等量级的交换,则时间复杂度为 O(n^2)。
平均情况下,需要 n*(n-1)/4 次交换操作,比较操作大于等于交换操作,而复杂度的上限是 O(n^2),所以平均情况下的时间复杂度就是 O(n^2)。
因为冒泡排序只是相邻元素之间的交换操作,只用到了常量级的额外空间,所以空间复杂度为 O(1)
那么冒泡排序是稳定的吗? 当然是稳定的,我们代码中,当 nums[j] > nums[j + 1] 时,才会进行交换,相等时不会交换,相等元素的相对位置没有改变,所以冒泡排序是稳定的。

简单选择排序(Simple Selection Sort)
我们的冒泡排序不断进行交换,通过交换完成最终的排序,我们的简单选择排序的思想也很容易理解,主要思路就是我们每一趟在 n-i+1 个记录中选取关键字最小的记录作为有序序列的第 i 个记录,见下图
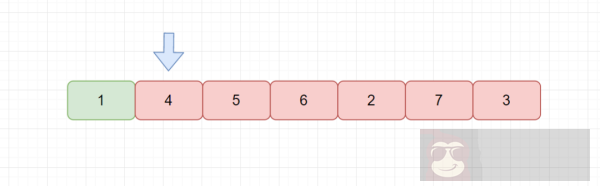
例如上图,绿色代表已经排序的元素,红色代表未排序的元素。我们当前指针指向 4,则我们遍历红色元素,从中找到最小值,然后与 4 交换。我们发现选择排序执行完一次循环也至少可以将 1 个元素归位。
下面我们来看一下代码的执行过程,看过之后肯定能写出代码的。
注:我们为了更容易理解,min 值保存的是值,而不是索引,实际代码中保存的是索引
简单选择排序代码
| class Solution {public int[] sortArray(int[] nums) { | |
| int len = nums.length; | |
| int min = 0; | |
| for (int i = 0; i nums[j]) min = j; | |
| } | |
| if (min != i) swap(nums,i,min); | |
| } | |
| return nums; | |
| } | |
| public void swap (int[] nums, int i, int j) {int temp = nums[i]; | |
| nums[i] = nums[j]; | |
| nums[j] = temp; | |
| } | |
| } |
从简单选择排序的过程来看,他最大的特点就是交换移动元素次数相当少,这样也就节省了排序时间,简单选择和冒泡排序不一样,我们发现无论最好情况和最坏情况,元素间的比较次数是一样的,第 i 次排序,需要 n – i 次比较,n 代表元素个数,则一共需要比较(n-1) + (n-2) +…. + 2 + 1= n*(n-1)/2 次。
对于交换而言,最好情况交换 0 次,最坏情况 (逆序时) 交换 n – 1 次。那么简单选择排序时间复杂度也为 O(n^2) 但是其交换次数远小于冒泡排序,所以其效率是好于冒泡排序的。
由我们的动图可知,我们的简单选择排序只用到了常量级的额外空间,所以空间复杂度为 O(1)。
我们思考一下,我们的简单选择排序是稳定的吗?
显然不是稳定的,因为我们需要在指针后面找到最小的值,与指针指向的值交换,见下图。
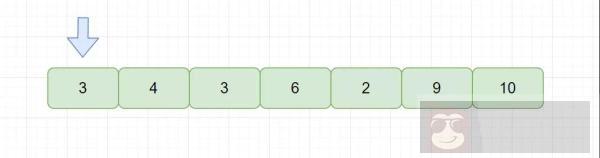
此时我们需要从后面元素中找到最小的元素与指针指向元素交换,也就是元素 2。但是我们交换后发现,两个相等元素 3 的相对位置发生了改变,所以简单选择排序是不稳定的排序算法。

















